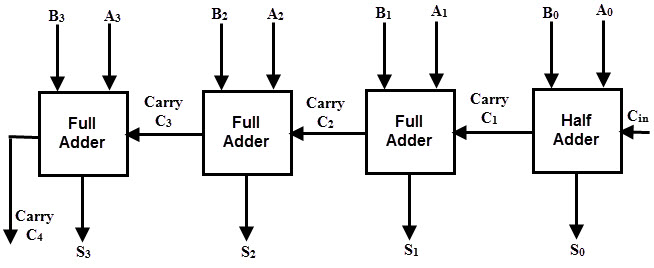
In such adder circuits, it is not possible to produce the sum and carry outputs of any stage until the input carry occurs. So there will be a considerable time delay in the addition process , which is known as , carry propagation delay. In any combinational circuit , signal must propagate through the gates before the correct output sum is available in the output terminals.
Consider the above figure, in which the sum S4 is produced by the corresponding full adder as soon as the input signals are applied to it. But the carry input C4 is not available on its final steady state value until carry c3 is available at its steady state value. Similarly C3 depends on C2 and C2 on C1. Therefore, carry must propagate to all the stages in order that output S4 and carry C5 settle their final steady-state value. The propagation time is equal to the propagation delay of the typical gate times the number of gate levels in the circuit. For example, if each full adder stage has a propagation delay of 20n seconds, then S4 will reach its final correct value after 80n (20 × 4) seconds. If we extend the number of stages for adding more number of bits then this situation becomes much worse. So the speed at which the number of bits added in the parallel adder depends on the carry propagation time. However, signals must be propagated through the gates at a given enough time to produce the correct or desired output. The following are the methods to get the high speed in the parallel adder to produce the binary addition. Back to top
Carry-Lookahead Adder
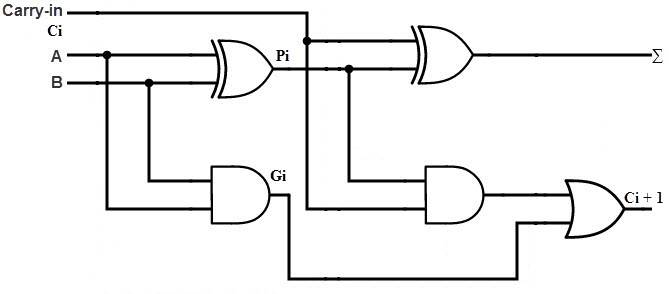
A carry-Lookahead adder is a fast parallel adder as it reduces the propagation delay by more complex hardware, hence it is costlier. In this design, the carry logic over fixed groups of bits of the adder is reduced to two-level logic, which is nothing but a transformation of the ripple carry design. This method makes use of logic gates so as to look at the lower order bits of the augend and addend to see whether a higher order carry is to be generated or not. Let us discuss in detail.
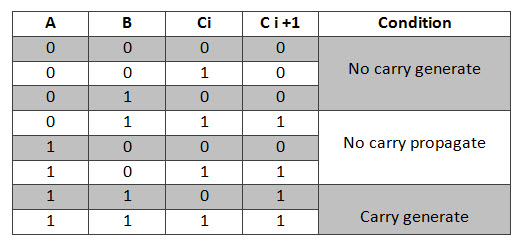
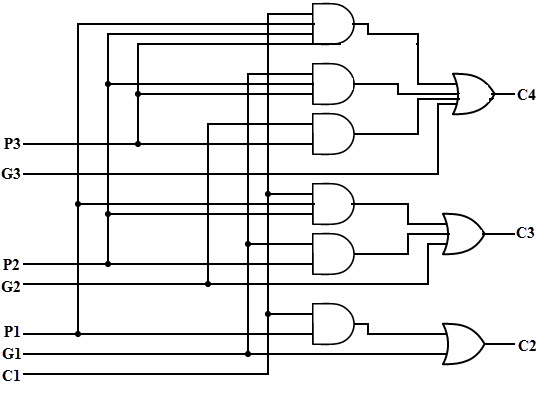
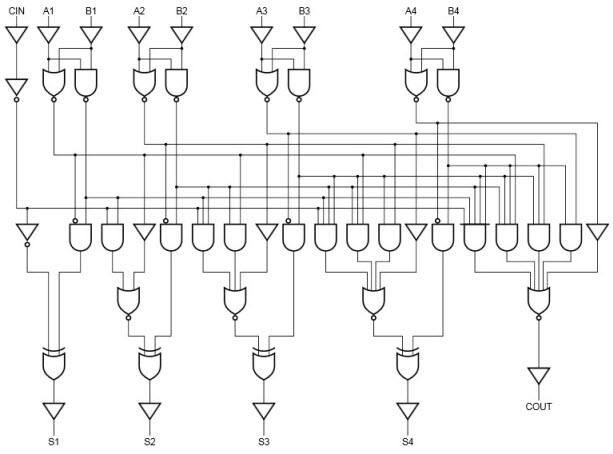
Consider the full adder circuit shown above with corresponding truth table. If we define two variables as carry generate Gi and carry propagate Pi then, Pi = Ai ⊕ Bi Gi = Ai Bi The sum output and carry output can be expressed as Si = Pi ⊕ Ci C i +1 = Gi + Pi Ci Where Gi is a carry generate which produces the carry when both Ai, Bi are one regardless of the input carry. Pi is a carry propagate and it is associate with the propagation of carry from Ci to Ci +1. The carry output Boolean function of each stage in a 4 stage carry-Lookahead adder can be expressed as C1 = G0 + P0 Cin C2 = G1 + P1 C1 = G1 + P1 G0 + P1 P0 Cin C3 = G2 + P2 C2 = G2 + P2 G1+ P2 P1 G0 + P2 P1 P0 Cin C4 = G3 + P3 C3 = G3 + P3 G2+ P3 P2 G1 + P3 P2 P1 G0 + P3 P2 P1 P0 Cin From the above Boolean equations we can observe that C4 does not have to wait for C3 and C2 to propagate but actually C4 is propagated at the same time as C3 and C2. Since the Boolean expression for each carry output is the sum of products so these can be implemented with one level of AND gates followed by an OR gate. The implementation of three Boolean functions for each carry output (C2, C3 and C4) for a carry-Lookahead carry generator shown in below figure.
Therefore, a 4 bit parallel adder can be implemented with the carry-Lookahead scheme to increase the speed of binary addition as shown in below figure. In this, two Ex-OR gates are required by each sum output. The first Ex-OR gate generates Pi variable output and the AND gate generates Gi variable. Hence, in two gates levels all these P’s and G’s are generated. The carry-Lookahead generators allows all these P and G signals to propagate after they settle into their steady state values and produces the output carriers at a delay of two levels of gates. Therefore, the sum outputs S2 to S4 have equal propagation delay times.
It is also possible to construct 16 bit and 32 bit parallel adders by cascading the number of 4 bit adders with carry logic. A 16 bit carry-Lookahead adder is constructed by cascading the four 4 bit adders with two more gate delays, whereas the 32 bit carry-Lookahead adder is formed by cascading of two 16 bit adders. In a 16 bit carry-Lookahead adder, 5 and 8 gate delays are required to get C16 and S15 respectively, which are less as compared to the 9 and 10 gate delay for C16 and S15 respectively in cascaded four bit carry-Lookahead adder blocks. Similarly, in 32 bit adder, 7 and 10 gate delays are required by C32 and S31 which are less compared to 18 and 17 gate delays for the same outputs if the 32 bit adder is implemented by eight 4 bit adders. Back to top
Carry-Lookahead Adder ICs
The high speed carry-Lookahead adders are integrated on integrated circuits in different bit configurations by several manufacturers. There are several individual carry generator ICs are available so that we have to make connection with logic gates to perform the addition operation. A typical carry-Lookahead generator IC is 74182 which accept four pairs of active low carry propagate (as P0, P1, P2 and P3) and carry generate (Go, G1, G2 and G3) signals and an active high input (Cn). It provides active high carriers (Cn+x, Cn+y, Cn+z) across the four groups of binary adders. This IC also facilitates the other levels of look ahead by active low propagate and carry generate outputs. The logic expressions provided by the IC 74182 are
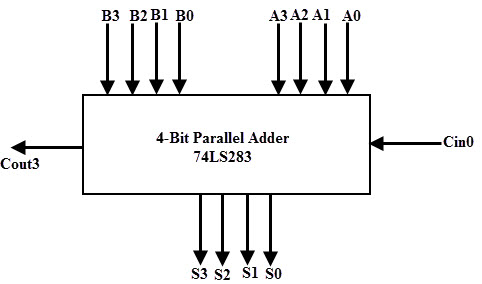
On the other hand, there are many high speed adder ICs which combine a set of full adders with carry-Lookahead circuitry. The most popular form of such IC is 74LS83/74S283 which is a 4 bit parallel adder high speed IC that contains four interconnected full adders with a carry-Lookahead circuitry. The functional symbol for this type of IC is shown in below figure. It accepts the two 4 bit numbers as A3A2A1A0 and B3B2B1B0 and input carry Cin0 into the LSB position. This IC produce output sum bits as S3S2S1S0 and the carry output Cout3 into the MSB position.
By cascading two or more parallel adder ICs we can perform the addition of larger binary numbers such as 8 bit, 24-bit and 32 bit addition. Back to top Comment * Name * Email * Website
Δ



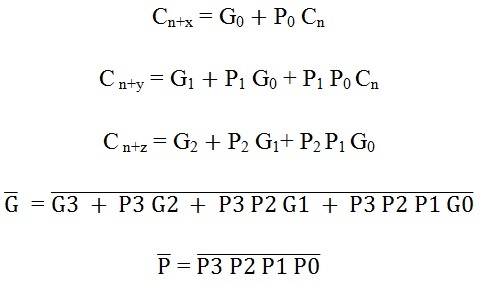



![]()